[Python]데이터 전처리 - 데이터 정제(2) 이상치 확인하기

엔피디 2024. 8. 10. 22:42

이번 포스팅에서는 이상치의 정의와 이상치를 확인하는 방법을 위주로 알아보겠습니다. 그리고 확인과정에서 필요한 seaborn 패키지의 박스플롯을 그리고, 박스플롯의 통계적 의미에 대해서도 소개하겠습니다.

실습준비

colab 실행

# 구글 드라이브 마운트
from google.colab import drive
drive.mount('/content/drive')

# 판다스 라이브러리
import pandas as pd

finalterm = pd.read_csv('finalterm.csv') # 파일경로
finalterm

이상치(Outlier)

이상치(Outlier)는 데이터 분석에서 일반적인 패턴에서 크게 벗어난 값이나 관측치를 의미합니다. 쉽게 말해 다른 데이터들과 동떨어진 너무 크거나 너무 작은 값입니다. 이러한 값은 데이터의 분포에서 크게 벗어나 있기 때문에 분석 결과에 큰 영향을 미칠 수 있습니다.

발생 이유

측정 오류 : 데이터 수집 과정에서 기기 오작동이나 사람의 실수로 인해 발생하는 잘못된 값입니다.
자연스러운 변동성 : 어떤 경우에는 특정 관측치가 다른 관측치와 유독 다를 수 있습니다. 즉, 정확하게 측정 되었지만 오류처럼 보이는 경우가 있습니다. 예를 들어, 키와 몸무게 데이터를 다룰 때 키가 매우 큰 사람이나 몸무게가 매우 적은 사람은 자연스럽게 이상치로 나타날 수 있습니다.
의도적인 조작 : 데이터가 악의적으로 변조된 경우에도 이상치가 발생할 수 있습니다.

이상치 확인의 중요성

분석 결과 왜곡 : 이상치는 평균, 표준편차 등 통계량에 큰 영향을 미쳐 분석 결과를 왜곡할 수 있습니다. 그래서 이상치를 확인하고 기준에 따라 처리하는 것이 중요합니다.
예시 상황 : 사람의 키 평균을 구하기 cm단위 데이터로 기록되어 있을 때, 이상치인 m단위 데이터가 하나만 존재하더라도 평균값이 극단적으로 낮아질 수 있습니다.

이상치 확인 방법

육안으로 확인하기(value_counts)

명확한 기준으로 데이터가 수집된 경우 육안으로도 이상치를 확인 가능한 경우가 있습니다.

# 육안으로 확인 가능한 경우
df = pd.DataFrame({'sex' : [1, 2, 2, 1, 3],
                   'height' : [178, 164, 159, 183, 1.74]})
df

남자를 1 여자를 2로 간주할 때 3은 이상치로 분류됩니다.

# value_count로 이상치 갯수 확인하기
df['sex'].value_counts()

그래프를 이용한 방법

박스플롯(Box plot), 산점도(Scatter plot) 등을 통해 데이터의 분포를 시각적으로 확인할 수 있습니다. seaborn 패키지를 통해 그래프를 쉽게 그릴 수 있습니다.

seaborn 패키지

seaborn은 데이터 시각화를 위한 고급 라이브러리입니다. Matplotlib을 기반으로 만들어졌으며, 더 간단하고 미적인 그래프를 쉽게 생성할 수 있도록 설계되었습니다. 데이터 분석과 시각화를 더욱 직관적이고 효율적으로 수행할 수 있게 해주는 매우 유용한 도구입니다.

박스플롯 그리기

# seaborn 패키지 불러오기
import seaborn as sns

사용 방법

sns.boxplot(데이터)

# 수학 과목 박스 플롯 그리기
sns.boxplot(finalterm['math'])

# 과학 과목 박스 플롯 그리기
sns.boxplot(finalterm['science'])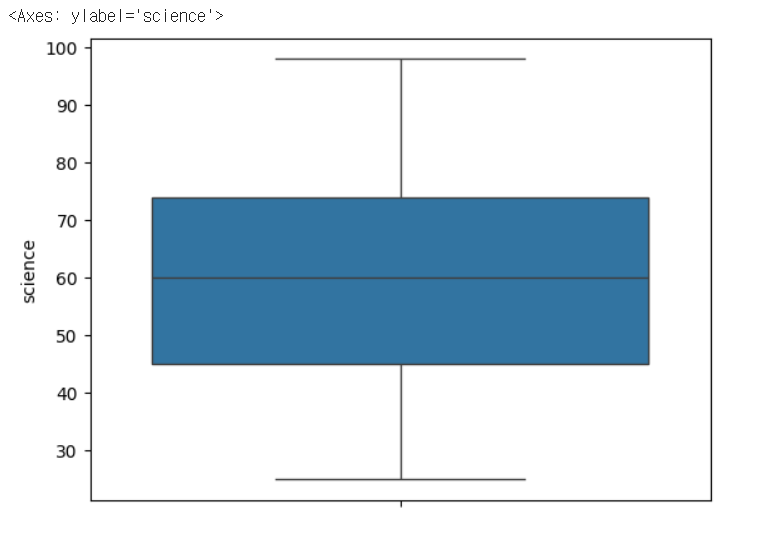

통계적 방법(IQR)

평균에서 3표준편차를 벗어난 데이터, 사분위수 범위(IQR)를 벗어난 데이터 등을 이상치로 판단할 수 있습니다.

사분위수 구하기

df.quantile(퍼센트)

# 하위 25% 1사분위수 구하기
Q1 = finalterm['math'].quantile(0.25)
Q1

50.0

# 하위 75% 3사분위수 구하기
Q3 = finalterm['math'].quantile(0.75)
Q3

72.5

# IQR 구하기
IQR = Q3 - Q1
IQR

22.5

# 상한선 구하기
upper_line = Q3 + 1.5 * IQR
upper_line

106.25(논리적으로 100점 이상이 존재하지 않지만, 임의의 데이터이기에 통계적 의미에서 정상범위로 간주)

# 하한선 구하기
lower_line = Q1 - 1.5 * IQR
lower_line

16.25

최종적으로 구한 상한선 보다 큰 값을 가지거나 하한선 보다 작은 값을 가지면 해당 데이터는 극단치(이상치)입니다. 즉, 상한선과 하한선 사이(IQR)은 정상 데이터 범주로 간주됩니다.

이상치를 처리하는 방법으로는 크게 3가지가 있는데요, 이번 포스팅에서 언급한 내용을 바탕으로 이상치 처리가 이루어지기에 오늘 학습한 내용을 기억하시면 좋을 것 같습니다. 다음 포스팅에서는 이상치 처리 방법에 대해 자세히 알아보겠습니다.